Matemáticas Simples

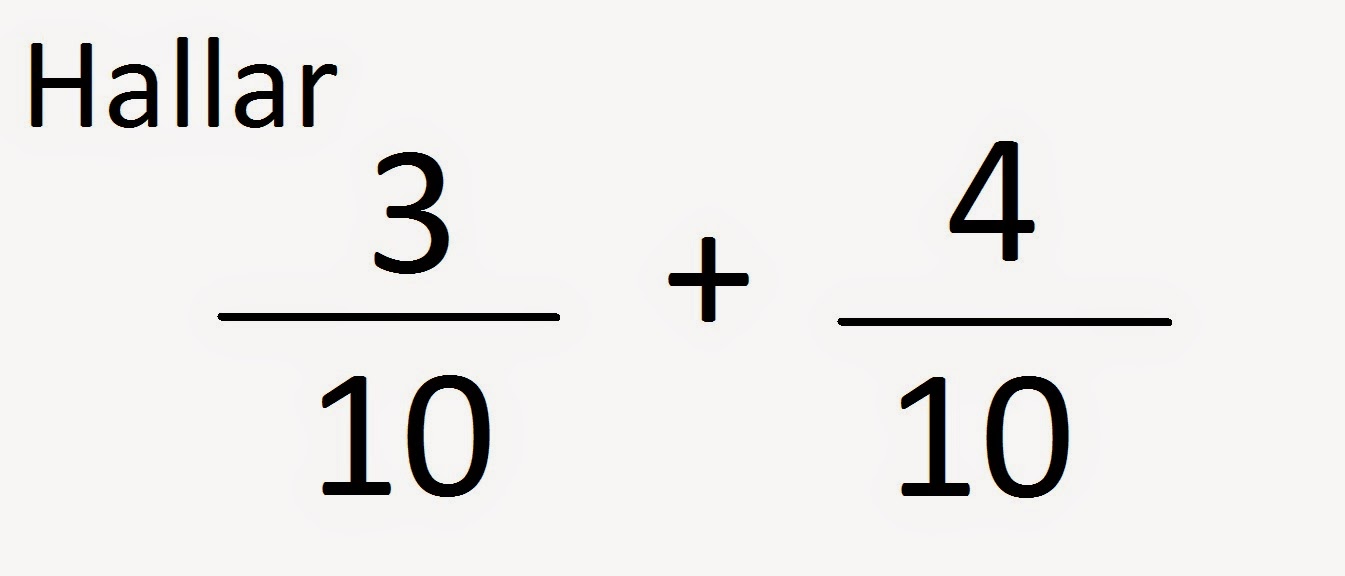
Hola amigos, empezaremos con adición de fracciones. Para un mejor entendimiento dividamos en dos casos: adición de fracciones homogéneas y adición de fracciones heterogéneas. ADICION DE FRACCIONES HOMOGENEAS Veamos cómo representamos gráficamente esta operación: Para hallar la suma de un par de fracciones homogéneas se halla la suma de los numeradores. Este resultado es el numerador de la fracción buscada cuyo denominador es el común de las fracciones dadas. Luego si es posible, se simplifica. ADICION DE FRACCIONES HETEROGENEAS Para hallar la suma de dos fracciones de este tipo se hallan las fracciones homogéneas equivalentes a las fracciones dadas y luego, las fracciones heterogéneas que son las resultantes, se suman. Veamos: Hallar:    2/5 + 4/9    2/5 + 4/9 = 2 x 9 / 5 x 9 + 4 x 5 / 9 x 5                   = 18 / 45 + 20 / 45                   = 38 / 45 Veamos otro ejemplo:   4/15 + 5/12 = 4 x 12 / 15 x 12 + 5 x 15 / 12 x 15                      = 48 / 180 + 75

Buen día matemáticos, en esta ocasión les explicaré cómo realizar la radicación en números enteros, veremos también las raíces cuadradas exactas e inexactas y por último la aplicación de la radicación a la geometría. Hemos visto que la potenciación en Z con exponente entero positivo es la operación en la que: dado un número entero cualquiera b, llamado base , y un entero positivo n, llamado exponente , se trata de hallar  su potencia b n . Así: Si b = 5 y n = 2, se trata de hallar 5 2 = 25 Si b = -5 y n = 2, se trata de hallar -5 2 = 25 Ahora nos interesa el caso en que: dada la potencia b n y el número entero positivo n , se trata de hallar el número entero b .A la operación que nos permite esto se llama radicación . Así: 25 y 2, se trata de hallar el 5 ó el -5 Esto se denota por: Para pasar de la potenciación a la radicación, ocurre que: La potencia a pasa a ser cantidad subradical o radicando . El exponente n pasa a ser índice de la raíz. La base

Recordemos que en números naturales (N) la potenciación es la operación que a cada par de números naturales b y n hace corresponder su potencia b n , donde b es la base y n , el exponente. b n significa que la base b se debe repetir n veces como factor. Así: 2 0 = 1 2 1 = 2 2 2 = 2 x 2 = 4                                       n veces 2 2 3 = 2 x 2 x 2 = 8 ……………………….. 2 = 2 x 2 x … x 2  b 0 = 1 b 1 = b b 2 = b x b                                             n veces b b 3 = b x b x b …………………….. b n = b x b x … x b Observamos que la potencia    b n , con b y n, números naturales, es un número natural. Vamos a considerar el caso en que la base b sea un número entero y el exponente un número entero positivo o número natural. 2 3 = 2 x 2 x 2 = 8 -2 3 = -2 x -2 x -2 = -8 3 4 = 3 x 3 x 3 x 3 = 81 -3 4 = -3 x -3 x -3 x -3 = 81 5 3 = 5 x 5 x 5 = 125 -5 3 = -5 x -5 x -5 = -125 PROPIEDADES: 1.La potencia

Para la división hay que tener en cuenta la ley de los signos , que se deduce de la ley de los signos de la multiplicación. Este cuadro quiere decir que el cociente de dos números del mismo signo es positivo y de signo contrario es negativo. Ejemplos: 30 : 5 = 6 48 : -6 = -8 -84 : 6 = -14 -78 : -6 = 13 -88 : -11 = 8 120 : -5 = -24 La expresión euclideana de la división con dividendo D , divisor d , cociente c y residuo r es: D = dc + r Ejemplos: 29 : 6 = 4 con 5 de residuo porque 29 = 6 x 4 + 5 29 : -6 = 5 con 5 de residuo porque 29 = -6 x -4 + 5 -29 : 6 = -4 con -5 de residuo porque -29 = 6 x -4 + -5 -29 : -6 = -4 con -5 de residuo porque -29 = 6 x -4 + -5 En otras palabras la división en N tiene el mismo proceso que la división en Z, sólo que en Z se le añaden signos (+ ó - ). Ejercicios: 1.Si D es el dividendo; d, el divisor; c, el cociente; y r, el residuo, completar la siguiente tabla con el o los términos que faltan: 2.¿El cociente de dos núm