Potenciación en números enteros Z con exponente entero positivo: propiedades y su aplicación a la geometría

-
Recordemos que en números naturales (N) la potenciación es la operación que a cada par de números naturales b y n hace corresponder su potencia bn, donde b es la base y n, el exponente.

bn significa que la base b se debe repetir n veces como factor.

Así:

20 = 1
21 = 2
22 = 2 x 2 = 4                                       n veces 2
23 = 2 x 2 x 2 = 8
………………………..
2 = 2 x 2 x … x 2 

b0 = 1
b1 = b
b2 = b x b                                             n veces b
b3 = b x b x b
……………………..
bn = b x b x … x b

Observamos que la potencia  bn, con b y n, números naturales, es un número natural.
Vamos a considerar el caso en que la base b sea un número entero y el exponente un número entero positivo o número natural.

23 = 2 x 2 x 2 = 8
-23 = -2 x -2 x -2 = -8
34 = 3 x 3 x 3 x 3 = 81
-34 = -3 x -3 x -3 x -3 = 81
53 = 5 x 5 x 5 = 125
-53 = -5 x -5 x -5 = -125

PROPIEDADES:

1.La potencia bn, con bn pertenece a Z y n pertenece +Z0, es un número entero.

Ejemplo:
-23 = -8            -53 = -125
42 = 16              54 = 625
-42 = 16            -63 = -216

2. Paridad del exponente y signo de la potencia.

Observando:
22 = 2 x 2 = 4
-22 = -2 x -2 = 4
23 = 2 x 2 x 2 = 8
-23 = -2 x -2 x -2 = -8
24 = 2 x 2 x 2 x 2 = 16
-24 = -2 x -2 x -2 x -2 = 16
25 = 2 x 2 x 2 x 2 x 2 = 32
-25 = -2 x -2 x -2 x -2 x -2 = -32

La potencia de cualquier número entero positivo es positiva.
La potencia par (cuando n es par) de cualquier número entero negativo es positivo y su potencia impar es negativa. Esto quiere decir que la potencia impar tiene el mismo signo que la base.

3.Producto de potencias de la misma base.

Observemos:
-23 x -22 = -2 x -2 x -2 x -2 x -2 = -25 = -23+2
-34 x -32 = -3 x -3 x -3 x -3 x -3 x -3 = -36 = -34+2
bm . bn = bm+n
El producto de potencias bm y bn de base b y exponentes m y n es la potencia bm+n, cuya base es b y exponente igual a la suma de los exponentes m y n.

4.Cociente de potencias de la misma base.

Observemos:
27 : 24 = 128 : 16 = 23 = 27-4
-27 : -24 = -128 : 16 = -23 = -27-4
45 : 43 = 1024 : 64 = 16 = -23 = -27-4
83 : 82 = 512 : 64 = 8 = 81 = 83-2
bm : bn = bm-n

El cociente de dos potencias de la misma base es igual a la potencia cuya base es la base común con exponente igual a la diferencia del exponente de la potencia dividendo menos el de la potencia divisor.

Recordar que para realizar el producto o el cociente de potencias de bases distintas no hay otra regla que efectuar las potencias y luego el producto o cociente respectivo.

5.Producto de potencias de bases diferentes y exponentes iguales.

32 x 22 = 3 x 3 x 2 x 2 = (3 x 2) x (3 x 2) = (3 x 2)2
53 x 43 = 5 x 5 x 5 x 4 x 4 x 4 = (5 x 4) x (5 x 4) x (5 x 4) = (5 x 4)3
85 x 95 = (8 x 9)5
27 x 57 = (2 x 5)7 = 107 = 10 000 000

am bm = (ab)m

El producto de potencias distintas y exponente iguales es igual a la potencia cuya base es el producto de las bases dadas y cuyo exponente es el exponente común.

6.Cociente de potencias de bases distintas y exponentes iguales.

63 : 23 = 216 : 8 = 27 = 33 = (6 : 2)3
152 : -52 = (15 : -5)2 = -32 = 9
184 : 94 = (18 : 9)4 = 24 = 16
am : bm = (a : b)m

El cociente de potencias de bases distintas y exponentes iguales es igual a la potencia cuya base es el cociente de las bases dadas y el exponente es el exponente común. 

7.Potencia de potencia

(23)2 = (23) x (23) = (2 x 2 x 2) x (2 x 2 x 2) = 26 = 23x2
(32)4 = 32x4 = 38 = 6 561

(bm)n = bmn

La potencia de potencia es igual a la potencia cuya base es la base dada y cuyo exponente es el producto de los exponentes dados.

APLICACION DE LA POTENCIACION A LA GEOMETRIA

Entre algunas de estas aplicaciones tenemos:
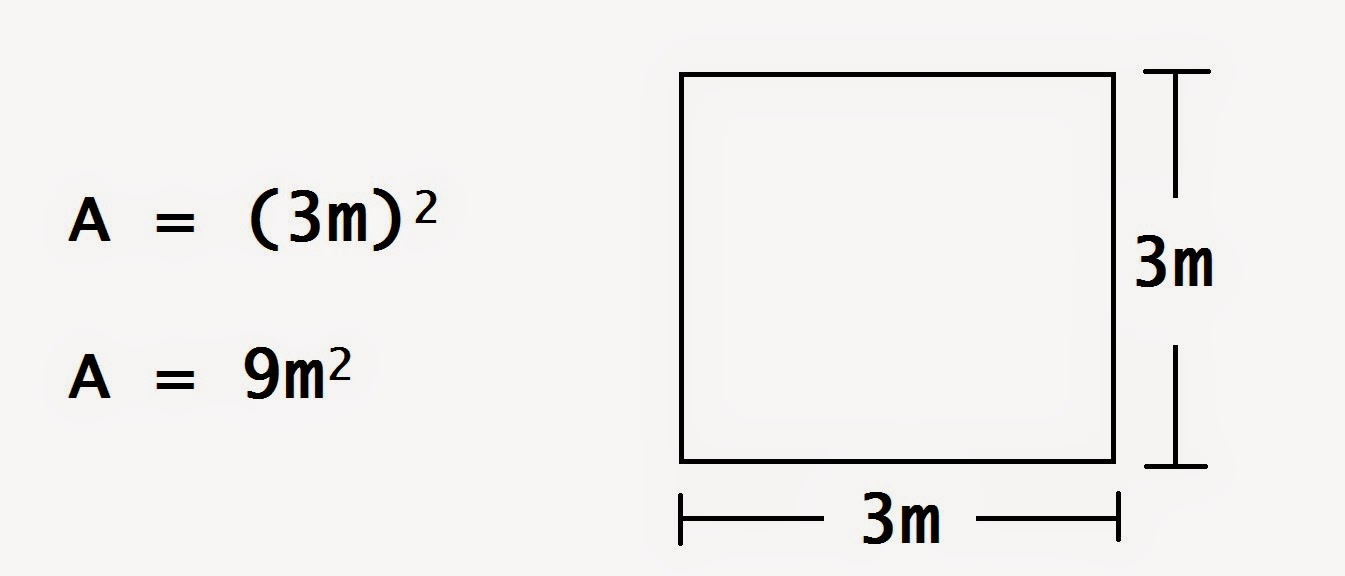
1.La potencia b2 se usa para calcular el área de un cuadrado de lado b.

Así:
El área de un cuadrado de 3m de lado es:
2.La potencia b3 se usa para calcular el volumen de un cubo de arista b. El volumen de un cubo de 4m de arista es:

Ejercicios:
1.Efectuar:
a) -62             e)36          i)-210      m)-84
b)-82              f)-36          j)210        n)85
c)-54              g)45          k)104       o)-123
d)28               h)-45         l)-124       p)-152

2.Completar la siguiente tabla:
3.Completar la siguiente tabla:
4.Efectuar:
a)23 + -32 + -52 -43
b)43 x 22 + 52 x -32 - 62 x -53
c)82 : 23 + 92 x -42 – 8 x -23 – 103 x 52
d)124 : 34 – 82 : 4 + 102 x 32 -73 x 42
e)105 : 55 - -93 x -42 + 26 : 42 + 53 x 42 -25 : 23
f)(38 x 32) : 37 + (-82 : 43) x 23 -102 x 30 - -83 : 8

5.¿Cuál es el área de un cuadrado de 10cm de lado?
6.¿Cuál es el área de un terreno cuadrangular de 20m de lado?
7.¿Cuánto vale un terreno cuadrado de 15m de lado, si el metro cuadrado está valorado a 80 nuevos soles?
8.¿Cuál es el área de un terreno rectangular de 20m de largo por 10m de ancho?
9.¿Cuál es el volumen de un cubo de 10cm de arista?

Si te gustó, compártelo 
¿Crees que me faltó algo?, deja tu comentario :)  

Comentarios

Publicar un comentario

Temas más buscados

Explorando el Teorema de Euclides: Relaciones de Ángulos y Lados en Triángulos

-
Imagen
Descifrando los Secretos de la Geometría Euclidiana: Aplicaciones Prácticas del Teorema de Euclides en la Vida Cotidiana El Teorema de Euclides , nombrado en honor al matemático griego Euclides de Alejandría , es uno de los resultados más fundamentales y conocidos en la geometría euclidiana. Este teorema establece una relación crucial entre los ángulos y los lados de un triángulo, lo que ha sido de gran importancia en la resolución de problemas geométricos desde la antigüedad. Acompáñanos en este fascinante recorrido mientras exploramos el Teorema de Euclides, presentamos ejemplos fáciles de entender y resolver, y descubrimos sus aplicaciones prácticas en nuestra vida diaria. El Teorema de Euclides se refiere a la suma de los ángulos internos de un triángulo, que siempre es igual a 180 grados. Matemáticamente, se expresa como: Ángulo A + Ángulo B + Ángulo C = 180° Donde Ángulo A, Ángulo B y Ángulo C representan los tres ángulos internos de un triángulo. Para comprender mejor el Teorem
Read more »

Radicación en números enteros Z

-
Imagen
Buen día matemáticos, en esta ocasión les explicaré cómo realizar la radicación en números enteros, veremos también las raíces cuadradas exactas e inexactas y por último la aplicación de la radicación a la geometría. Hemos visto que la potenciación en Z con exponente entero positivo es la operación en la que: dado un número entero cualquiera b, llamado base , y un entero positivo n, llamado exponente , se trata de hallar  su potencia b n . Así: Si b = 5 y n = 2, se trata de hallar 5 2 = 25 Si b = -5 y n = 2, se trata de hallar -5 2 = 25 Ahora nos interesa el caso en que: dada la potencia b n y el número entero positivo n , se trata de hallar el número entero b .A la operación que nos permite esto se llama radicación . Así: 25 y 2, se trata de hallar el 5 ó el -5 Esto se denota por: Para pasar de la potenciación a la radicación, ocurre que: La potencia a pasa a ser cantidad subradical o radicando . El exponente n pasa a ser índice de la raíz. La base
Read more »

Números mixtos y fracciones impropias

-
Imagen
Una forma abreviada de escribir a + b/c es a b/c A estos números a b/c , formado por una parte entera y una fracción, llamamos número mixto . Son números mixtos: Sabemos que una fracción impropia es aquella cuyo numerador es mayor que su denominador. El valor de una fracción impropia es mayor que 1, por tanto puede escribirse como un número mixto. Para convertir una fracción en un número mixto se divide el numerador entre el denominador. El cociente es la parte entera del número mixto y la fracción tiene como numerador el residuo de la división y como denominador, el mismo denominador de la fracción impropia dada. Ejemplos:  Convertir 27/4 Convertir 68/28 a número mixto. Para convertir un número mixto a b/c a fracción impropia se procede como sigue: Un número mixto es igual a una fracción impropia cuyo numerador es igual al producto de la parte entera por el denominador de la parte fraccionaria más el numerador de esta y cuyo denominador es el
Read more »

Fracciones: definición, clases de fracciones, simplificación de fracciones

-
Imagen
Llamamos fracciones al número de la forma ( a/b ) siendo a y b números enteros, con b  ≠ 0. El numerador es a y b, el denominador. El denominador b  indica las partes iguales en las que se ha dividido la unidad y el numerador a  indica que de estas partes iguales se han tomado a de ellas. Así, en 5/2 el numerador es 5 y el denominador, 2. En este caso, 2 indica que la unidad se ha dividido en 2 partes iguales y el 5, que de esas 2 partes se han tomado 5. Las fracciones pueden ser positivas tales como 2/4, 3/5, 7/2, etc; y negativas tales como -4/5, -3/6, -7/8, etc. Las fracciones se representan mediante figuras geométricas o en la recta numérica como vemos a continuación: Como vemos en los gráficos, la representación de las fracciones sobre la recta numérica nos ofrece la ventaja de poder representar fracciones tanto positivas como negativas. Cuando se desea representar una fracción determinada sobre la recta numérica tal como 2/3, 5/4 y -3/4 se procede así:
Read more »

División de números enteros

-
Imagen
Para la división hay que tener en cuenta la ley de los signos , que se deduce de la ley de los signos de la multiplicación. Este cuadro quiere decir que el cociente de dos números del mismo signo es positivo y de signo contrario es negativo. Ejemplos: 30 : 5 = 6 48 : -6 = -8 -84 : 6 = -14 -78 : -6 = 13 -88 : -11 = 8 120 : -5 = -24 La expresión euclideana de la división con dividendo D , divisor d , cociente c y residuo r es: D = dc + r Ejemplos: 29 : 6 = 4 con 5 de residuo porque 29 = 6 x 4 + 5 29 : -6 = 5 con 5 de residuo porque 29 = -6 x -4 + 5 -29 : 6 = -4 con -5 de residuo porque -29 = 6 x -4 + -5 -29 : -6 = -4 con -5 de residuo porque -29 = 6 x -4 + -5 En otras palabras la división en N tiene el mismo proceso que la división en Z, sólo que en Z se le añaden signos (+ ó - ). Ejercicios: 1.Si D es el dividendo; d, el divisor; c, el cociente; y r, el residuo, completar la siguiente tabla con el o los términos que faltan: 2.¿El cociente de dos núm
Read more »