Resolución de ecuaciones con una variable de primer grado
Resolver una ecuación es hallar el valor o valores de la variable que hacen verdadero el enunciado abierto por ella representada.
El valor o valores de la variable que hacen verdadero este enunciado abierto se dice que satisfacen la ecuación y constituyen la solución de la misma.
El conjunto de todos los valores de la variable que son solución de la ecuación se denomina conjunto solución.
En esta entrada resolveremos ecuaciones con una variable o incógnita, de primer grado, cuya solución, si existe, es única. Partiremos planteando problemas cuya solución será simplificada si utilizamos y resolvemos ecuaciones formuladas como una traducción simbólica del enunciado verbal de dichos problemas. Haremos esto con el objeto de hacer notar que muchísimos problemas matemáticos se resuelven a través de ecuaciones y hacer ver la urgente necesidad que tenemos de aprender a resolverlos.
Es importante tener en cuenta que en el proceso de solución de una ecuación sólo usaremos las propiedades de las operaciones con números naturales y enteros relacionados con la igualdad y, en última instancia, la aproximación decimal, si la variable no resulta ser entera. Estos problemas, como se ve a continuación, son presentados en forma de adivinanzas o haciendo alusión real y cotidiana.
PROBLEMAS TIPO
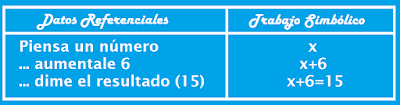
1. Luis: Pepe piensa un número, auméntale 6 y dime el resultado.
Pepe: 15
Luis: Pensaste 14
Pepe: Si, adivinaste.
2. Luis: Piensa un número, multiplícalo por 2, súmale 10 y dime el resultado.
Pepe: 26
Luis: Pensaste 8
Pepe: Cierto, ¿Cómo haces para adivinar?
Luis: Formo una ecuación y la resuelvo. ¿Quieres aprender?
Pepe: ¡Si, quiero pasar por adivino con cosas más complicadas!
Luis: Veamos cómo ordenamos el trabajo para cada caso.
1. Para la primera adivinanza se procede como sigue:
Resolviendo la ecuación formada:
Respuesta: El número pensado por Pepe es 9.
2. Para la segunda adivinanza se tiene:
Resolviendo la ecuación formada:
Respuesta: El número pensado por Pepe es 8.
3. Luis: ¿Quieres que adivine tu edad?
Multiplica tu edad por 3, réstale 8 y dime el resultado.
Pepe: 28
Luis: Tu edad es 12 años.
Pepe: Así es, ¿Cómo haces ahora?
Luis: Veamos.
Resolviendo la ecuación formada:
4. Si tuviera el triple que tengo y si mi padre me diera 40 soles, tendría los 400 soles que necesito, ¿Cuánto tengo?
Resolviendo la ecuación formada:
Respuesta: Tiene 120 soles.
5. Una revista de Historia y uno de Lenguaje cuestan 30 soles. Si la revista de Historia cuesta 2 soles más que el de Lenguaje, ¿Cuánto cuesta cada revista?
Resolviendo la ecuación:
Entendiste este tema?
¿Qué es resolver una ecuación?
¿A qué llamamos solución de una ecuación?
¿Qué es el conjunto solución de una ecuación?
Ejercicios:
1. Resolver los siguientes ejercicios:
a) x+7=16
b) x-5=11
c) x+2=42
d) x-14=18
e) 2x+8-x=15
f) 3x-10=x+8
g) 2x+8=x+20
h) 3x-12=2x+16
i) 2x+5=17
j) 2x-13=31
k) 3x+7=49
l) 3x-10=50
m) x+x+1=41
n) x+x-1=49
o) 2x+6=3x-9
p) 5x-18=3x+12
q) 2(x+8)=36
r) 3(x-2)=18
s) 3x-10-2x=15
t) 3(2x-11)=5x-3
2. ¿Cuál es el número que aumentado en 11 es 21?
3. ¿Cuál es el número que restado en 10 es 14?
4. La edad de Nelly aumentada en 8 años es 20. ¿Qué edad tiene?
5. La edad de Ricardo disminuida en 5 años es 25. ¿Cuál es su edad?
6. La edad de Juan dentro de 10 años será 36. ¿Qué edad tiene actualmente?
7. La edad de Carmen hace 8 años era 27. ¿Qué edad tiene ahora?
8. El dinero de Manuel aumentado en 500 soles es 2500 soles. ¿Cuánto tiene?
9. El doble de un número aumentado en 7 es 23. ¿Cuál es el número?
10. El triple de la edad de Victor disminuido en 4 años es 35. ¿Qué edad tiene?
11. Jorge es 2 años mayor que Silvia. Si ambas edades suman 20 años, ¿Qué edad tiene cada uno?
12. La suma de las edades de Daniel y Ricardo es 29 años. Si Daniel lleva en un año a Ricardo, ¿Qué edad tiene cada uno?
13. La suma de dos números consecutivos es 43 ¿Cuáles son los números?
14. La suma de dos números pares consecutivos es 34. ¿Cuáles son los números?
15. La suma de dos números impares consecutivos es 32. ¿Cuáles son los números?
16. La suma de tres números consecutivos es 30. Hallar los números.
17. En un colegio hay 580 alumnos. Si hay 20 varones más que mujeres, ¿Cuántos alumnos y alumnas hay?
18. He pensado un número que multiplicándolo por 3 y restando 5 al resultado, se obtiene 25. ¿Cuál es el número?
19. He pensado un número que multiplicado por 8 y sumando 10 al resultado, se obtiene 170, ¿Cuál es ese número?
20. Las edades de Teresa y de su hija suman 48 años. Si la de Teresa excede en 28 años a la de su hija, ¿Qué edad tiene cada una?
21. Un lapicero y un libro han costado 24 soles. Si el lapicero cuesta el triple que el libro, ¿Cuánto vale cada uno?
22. Se ha comprado un libro y un reloj por 60 soles. Si el costo del reloj es cuatro veces el del libro, ¿Cuánto vale cada uno?
23. Un hotel de dos pisos tiene 54 habitaciones. Si las del primero duplican en número a las del segundo, ¿Cuántas habitaciones tiene cada piso?
24. El mayor de dos números es cinco veces el menor y ambos suman 240. Hallar los números.
25. La edad de Consuelo es el triple de la de su hija, más 4 años. Si ambas edades suman 52, ¿Qué edad tiene cada una?
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)
El valor o valores de la variable que hacen verdadero este enunciado abierto se dice que satisfacen la ecuación y constituyen la solución de la misma.
El conjunto de todos los valores de la variable que son solución de la ecuación se denomina conjunto solución.
En esta entrada resolveremos ecuaciones con una variable o incógnita, de primer grado, cuya solución, si existe, es única. Partiremos planteando problemas cuya solución será simplificada si utilizamos y resolvemos ecuaciones formuladas como una traducción simbólica del enunciado verbal de dichos problemas. Haremos esto con el objeto de hacer notar que muchísimos problemas matemáticos se resuelven a través de ecuaciones y hacer ver la urgente necesidad que tenemos de aprender a resolverlos.
Es importante tener en cuenta que en el proceso de solución de una ecuación sólo usaremos las propiedades de las operaciones con números naturales y enteros relacionados con la igualdad y, en última instancia, la aproximación decimal, si la variable no resulta ser entera. Estos problemas, como se ve a continuación, son presentados en forma de adivinanzas o haciendo alusión real y cotidiana.
PROBLEMAS TIPO
1. Luis: Pepe piensa un número, auméntale 6 y dime el resultado.
Pepe: 15
Luis: Pensaste 14
Pepe: Si, adivinaste.
2. Luis: Piensa un número, multiplícalo por 2, súmale 10 y dime el resultado.
Pepe: 26
Luis: Pensaste 8
Pepe: Cierto, ¿Cómo haces para adivinar?
Luis: Formo una ecuación y la resuelvo. ¿Quieres aprender?
Pepe: ¡Si, quiero pasar por adivino con cosas más complicadas!
Luis: Veamos cómo ordenamos el trabajo para cada caso.
1. Para la primera adivinanza se procede como sigue:
Resolviendo la ecuación formada:
Respuesta: El número pensado por Pepe es 9.
2. Para la segunda adivinanza se tiene:
Resolviendo la ecuación formada:
Respuesta: El número pensado por Pepe es 8.
3. Luis: ¿Quieres que adivine tu edad?
Multiplica tu edad por 3, réstale 8 y dime el resultado.
Pepe: 28
Luis: Tu edad es 12 años.
Pepe: Así es, ¿Cómo haces ahora?
Luis: Veamos.
Resolviendo la ecuación formada:
4. Si tuviera el triple que tengo y si mi padre me diera 40 soles, tendría los 400 soles que necesito, ¿Cuánto tengo?
Resolviendo la ecuación formada:
Respuesta: Tiene 120 soles.
5. Una revista de Historia y uno de Lenguaje cuestan 30 soles. Si la revista de Historia cuesta 2 soles más que el de Lenguaje, ¿Cuánto cuesta cada revista?
Resolviendo la ecuación:
Entendiste este tema?
¿Qué es resolver una ecuación?
¿A qué llamamos solución de una ecuación?
¿Qué es el conjunto solución de una ecuación?
Ejercicios:
1. Resolver los siguientes ejercicios:
a) x+7=16
b) x-5=11
c) x+2=42
d) x-14=18
e) 2x+8-x=15
f) 3x-10=x+8
g) 2x+8=x+20
h) 3x-12=2x+16
i) 2x+5=17
j) 2x-13=31
k) 3x+7=49
l) 3x-10=50
m) x+x+1=41
n) x+x-1=49
o) 2x+6=3x-9
p) 5x-18=3x+12
q) 2(x+8)=36
r) 3(x-2)=18
s) 3x-10-2x=15
t) 3(2x-11)=5x-3
2. ¿Cuál es el número que aumentado en 11 es 21?
3. ¿Cuál es el número que restado en 10 es 14?
4. La edad de Nelly aumentada en 8 años es 20. ¿Qué edad tiene?
5. La edad de Ricardo disminuida en 5 años es 25. ¿Cuál es su edad?
6. La edad de Juan dentro de 10 años será 36. ¿Qué edad tiene actualmente?
7. La edad de Carmen hace 8 años era 27. ¿Qué edad tiene ahora?
8. El dinero de Manuel aumentado en 500 soles es 2500 soles. ¿Cuánto tiene?
9. El doble de un número aumentado en 7 es 23. ¿Cuál es el número?
10. El triple de la edad de Victor disminuido en 4 años es 35. ¿Qué edad tiene?
11. Jorge es 2 años mayor que Silvia. Si ambas edades suman 20 años, ¿Qué edad tiene cada uno?
12. La suma de las edades de Daniel y Ricardo es 29 años. Si Daniel lleva en un año a Ricardo, ¿Qué edad tiene cada uno?
13. La suma de dos números consecutivos es 43 ¿Cuáles son los números?
14. La suma de dos números pares consecutivos es 34. ¿Cuáles son los números?
15. La suma de dos números impares consecutivos es 32. ¿Cuáles son los números?
16. La suma de tres números consecutivos es 30. Hallar los números.
17. En un colegio hay 580 alumnos. Si hay 20 varones más que mujeres, ¿Cuántos alumnos y alumnas hay?
18. He pensado un número que multiplicándolo por 3 y restando 5 al resultado, se obtiene 25. ¿Cuál es el número?
19. He pensado un número que multiplicado por 8 y sumando 10 al resultado, se obtiene 170, ¿Cuál es ese número?
20. Las edades de Teresa y de su hija suman 48 años. Si la de Teresa excede en 28 años a la de su hija, ¿Qué edad tiene cada una?
21. Un lapicero y un libro han costado 24 soles. Si el lapicero cuesta el triple que el libro, ¿Cuánto vale cada uno?
22. Se ha comprado un libro y un reloj por 60 soles. Si el costo del reloj es cuatro veces el del libro, ¿Cuánto vale cada uno?
23. Un hotel de dos pisos tiene 54 habitaciones. Si las del primero duplican en número a las del segundo, ¿Cuántas habitaciones tiene cada piso?
24. El mayor de dos números es cinco veces el menor y ambos suman 240. Hallar los números.
25. La edad de Consuelo es el triple de la de su hija, más 4 años. Si ambas edades suman 52, ¿Qué edad tiene cada una?
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)














Comentarios
Publicar un comentario