Fracciones: definición, clases de fracciones, simplificación de fracciones
Llamamos fracciones al número de la forma ( a/b ) siendo a y b números enteros, con b
≠ 0. El numerador es a y b, el denominador.
El denominador b indica las partes iguales en las que se ha dividido la unidad y el numerador a indica que de estas partes iguales se han tomado a de ellas.
Así, en 5/2 el numerador es 5 y el denominador, 2. En este caso, 2 indica que la unidad se ha dividido en 2 partes iguales y el 5, que de esas 2 partes se han tomado 5.
Las fracciones pueden ser positivas tales como 2/4, 3/5, 7/2, etc; y negativas tales como -4/5, -3/6, -7/8, etc.
Las fracciones se representan mediante figuras geométricas o en la recta numérica como vemos a continuación:
Como vemos en los gráficos, la representación de las fracciones sobre la recta numérica nos ofrece la ventaja de poder representar fracciones tanto positivas como negativas. Cuando se desea representar una fracción determinada sobre la recta numérica tal como 2/3, 5/4 y -3/4 se procede así:
Las fracciones pueden ser:
Propias, si el numerador es menor que el denominador.
Impropias, se el numerador es mayor que el denominador.
Las fracciones propias pueden ser: 2/3, 5/8, 8/13, 1/20, etc.
Las fracciones impropias pueden ser: 3/2, 6/4, 8/2, 7/3, etc.
Además, si se comparan los denominadores de dos fracciones se tiene:
Fracciones homogéneas, si los denominadores son iguales.
Fracciones heterogéneas, si los denominadores son distintos.
Son homogéneos 5/4 y 3/4
Son heterogéneos 5/9 y 3/8
Fracciones equivalentes
En esta imagen vemos que, 1/2 y 3/6 están representados por los mismos puntos en la recta numérica, también representan la misma parte de la unidad. Por esto decimos que 1/2 y 3/6 son fracciones equivalentes y escribimos 1/2 ~ 3/6, aunque en ocasiones se escribe 1/2 = 3/6
También son equivalentes:
1/4 y 2/8, 1/3 y 2/6, 1/2 y 2/4, 1/2 y 4/8, 2/3 y 4/6, 3/4 y 6/8
SIMPLIFICACION DE FRACCIONES
Simplificar una fracción es hallar su fracción equivalente irreductible, esto es, una fracción equivalente a la dada cuyos términos sean primos entre sí.
Para simplificar 8/16 se divide 8 y 16 entre su m.c.d.
entonces se tiene 8/16 ~ 1/2, siendo 1/2 la fracción irreductible equivalente a 8/16.
Para simplificar 12/20 se tiene que su m.c.d. (12,20)=4 y por tanto:
Otra forma de simplificar una fracción, y la que uso más, es la de ir dividiendo simultáneamente al numerador y denominador entre sus divisores comunes.
Para simplificar 12/20 se tiene:
Aquí se dice que la mitad de 12 es 6 y de 20, 10; mitad de 6 es 3 y de 10, 5.
Ahora es el turno de ustedes usando el mismo método para las siguientes 4 simplificaciones.
Más temas de Fracciones:
¿Crees que me faltó algo?, deja tu comentario :)


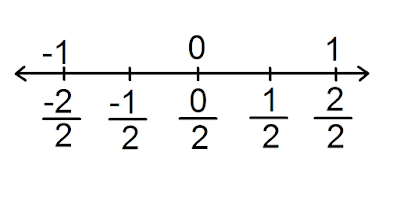














Comentarios
Publicar un comentario