Operaciones con conjuntos: intersección, unión y diferencia

Primero veremos la intersección de conjuntos, que están incluidos las propiedades. Luego veremos la unión de conjuntos y también lo que es la diferencia de conjuntos.

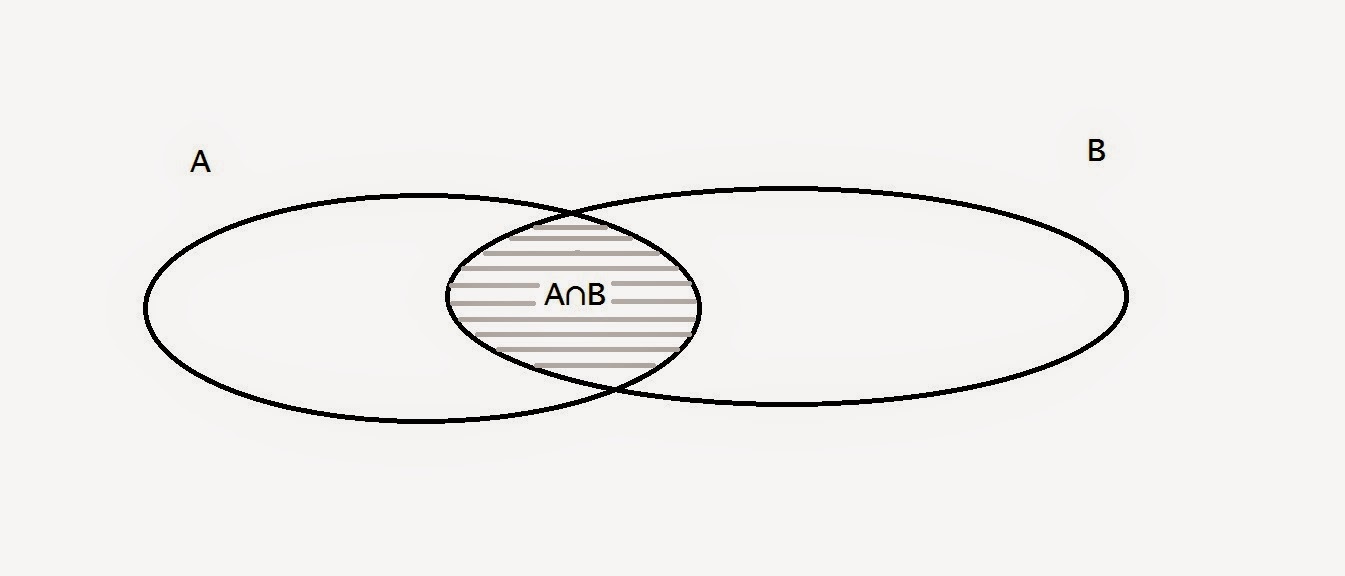
La intersección de los conjuntos A y B es el conjunto formado por los elementos de A que pertenecen a B.

A∩B se lee: A intersección B.

A∩B = {x/x ∈ A ∧ x ∈ B}

El símbolo ∧ se lee: y.

A ∩ B está formado por los elementos comunes a A y a B.

Veamos:

Si A = {1 , 2 , 3 , 4} y B = {2 , 4 , 6} , entonces A ∩ B = {2 , 4}

PROPIEDADES DE LA INTERSECCION

1.La intersección de dos conjuntos está incluida en cualquiera de ellos.
A ∩ B ⊂ A
A ∩ B ⊂ B
2.Si un conjunto está incluido en otro, entonces la intersección de ambos es el primero.

Las siguientes afirmaciones son consecuencia de esta propiedad:

Ø ∩ A = Ø  pues Ø ⊂ A

A ∩ A = A   ya que A ⊂ A

A ∩ U = A   porque A ⊂ U

Ahora veremos lo que es Unión de Conjuntos.

Supongamos que tenemos los conjuntos A y B, la union de los conjuntos A y B es el conjunto formado por los elementos que pertenecen al menos a uno de ellos.

Para que se capte mejor te lo ilustro:

El símbolo "v" se lee: o,y es incluyente en el sentido siguiente: afirmar que un elemento pertenece a A ó a B, que equivale a afirmar que pertenece al menos a uno de los dos conjuntos.

PROPIEDADES DE LA UNION

1.La unión de dos conjuntos incluye a cada uno de ellos.

A ⊂ A U B

B ⊂ A U B 

2.Si un conjunto A está incluido en un conjunto B, entonces la unión de ambos es B.

A ⊂ B = A U B = B

De esta propiedad se deducen:

Ø U A = A   pues   Ø ⊂ A

A U A = A   porque A ⊂ A

A U U = U   ya que A ⊂ U

Ahora toca lo que es Diferencia de conjuntos.
Bueno seguimos con los mismos conjuntos A y B, que estan formados por los elementos de A que no pertenecen a B.
Así:

A - B se lee: A menos B

A - B = { x/x ∈ A ∧ x ∉ B}

PROPIEDADES DE LA DIFERENCIA

1.La diferencia de conjuntos no es conmutativa. O sea A - B ≠ B - A

                                      

                                       

La unión y la intersección si es conmutativa, lo que se simboliza de la siguiente manera:

A U B = B U A

A ∩ B = B ∩ A 

2.Si dos conjuntos son disjuntos, entonces su diferencia es el primero.

A ∩ B = ∅ ⇒ A - B = A 

3.Si un conjunto A está incluido en un conjunto B, entonces la diferencia entre el primero y el segundo es el conjunto vacío.

A ⊂ B ⇒ A - B = ∅, ya que no existe ningún elemento de A que no pertenezca a B.}

Bueno público esto fue OPERACIONES CON CONJUNTOS, espero les guste.

Quiero aprovechar este post, ya que es el primero después de un largo tiempo de para, en agradecerles por las visitas, durante ese tiempo que no publiqué, noté que este blog era visitado frecuentemente.

Muchas gracias, siento que el blog es de gran ayuda y se siente bien contribuir, apoyar a los demás, gracias nuevamente.

Ejercicios de Conjuntos AQUÍ.

Si te gustó, compártelo 
¿Crees que me faltó algo?, deja tu comentario :)