Números racionales Q
En la figura de fracciones equivalentes observamos que el conjunto:
está formado por todas las fracciones equivalentes a 1/2. Todas estas fracciones son equivalentes entre sí.
Otros conjuntos de fracciones equivalentes pueden ser:
A cada uno de estos conjuntos de fracciones equivalentes llamamos número racional.
Como representante de un número racional puede tomarse cualquiera de sus fracciones, pero por lo general se toma la fracción irreductible. Así, los números racionales anteriores denotamos por:
Llamamos número racional [a/b] al conjunto de todas las fracciones equivalentes a la fracción a/b, en las que a y b son números enteros, con b ≠0.
Todos los números racionales conforman el conjunto Q de números racionales.
Se denota +Q al conjunto de números racionales positivos y -Q al de números racionales negativos.
En la figura se puede observar la representación de algunos números racionales.
En la práctica usamos sólo los representantes de los números racionales, que son las fracciones.
Pero también hay números que no es posible representarlos por una fracción y que se dice que son irracionales, cuyo conjunto se denota con Q'.
A la reunión de Q con Q' se denomina conjunto de los números reales y se denota con R.
COMPARACION DE NUMEROS REALES
Para comparar dos números reales se comparan sus representantes o fracciones. Sabemos que de dos números representados sobre la recta numérica, es mayor el que está ubicado a la derecha del otro y es menor el que está a la izquierda. Observando esa representación de las fracciones equivalentes se puede escribir:
1/2 < 3/4 , 7/8 > 3/4 , -3/4 < 1/2 , -5/8 < 1/8 , -1/2 > -5/8
Se observa que:
1/2 < 3/4 y 1 x 4 < 2 x 3 porque 4 < 6
-1/2 > -5/6 y -1 x 8 > 2 x (-5) porque -8 > -10
Entonces por lo general:
Esto es equivalente a decir que para comparar dos fracciones podemos tener en cuenta:
Si las fracciones tienen un denominador común (iguales) se comparan los numeradores.
Si tienen distintos denominadores tales como a/b y c/d se comparan las fracciones a x d / b x d y b x c / b x d que son equivalentes a las dadas, pero estas últimas tienen igual denominador.
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)
Otros conjuntos de fracciones equivalentes pueden ser:
Como representante de un número racional puede tomarse cualquiera de sus fracciones, pero por lo general se toma la fracción irreductible. Así, los números racionales anteriores denotamos por:
Todos los números racionales conforman el conjunto Q de números racionales.
Se denota +Q al conjunto de números racionales positivos y -Q al de números racionales negativos.
Pero también hay números que no es posible representarlos por una fracción y que se dice que son irracionales, cuyo conjunto se denota con Q'.
A la reunión de Q con Q' se denomina conjunto de los números reales y se denota con R.
COMPARACION DE NUMEROS REALES
Para comparar dos números reales se comparan sus representantes o fracciones. Sabemos que de dos números representados sobre la recta numérica, es mayor el que está ubicado a la derecha del otro y es menor el que está a la izquierda. Observando esa representación de las fracciones equivalentes se puede escribir:
1/2 < 3/4 , 7/8 > 3/4 , -3/4 < 1/2 , -5/8 < 1/8 , -1/2 > -5/8
Se observa que:
1/2 < 3/4 y 1 x 4 < 2 x 3 porque 4 < 6
-1/2 > -5/6 y -1 x 8 > 2 x (-5) porque -8 > -10
Entonces por lo general:
Si las fracciones tienen un denominador común (iguales) se comparan los numeradores.
Si tienen distintos denominadores tales como a/b y c/d se comparan las fracciones a x d / b x d y b x c / b x d que son equivalentes a las dadas, pero estas últimas tienen igual denominador.
Más temas de Fracciones:
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)
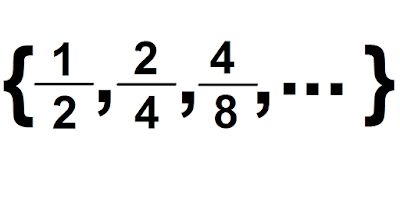










Comentarios
Publicar un comentario