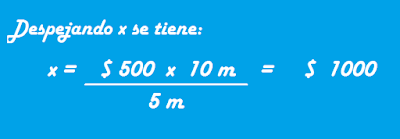
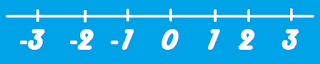
Ejercicios de Conjuntos - Parte 1
En esta parte les mostraré ejercicios relacionado a los Conjuntos . Empezando de lo más a simple a lo complejo. 1. Indicar cuáles de las siguientes expresiones definen conjuntos y cuáles no: - El conjunto formado por las últimas letras del abecedario. - El conjunto formado por los tres primeros números naturales. - El conjunto formado por los números naturales menores que 4. 2. Decir cuáles de las siguientes expresiones definen conjuntos y cuáles no: - El conjunto formado por todos los conjuntos. - El conjunto formado por algunos planetas. - El conjunto formado por el conjunto vacío. - El conjunto formado por el número cero. - El conjunto formado por los números pares y el rector de un colegio determinado. - El conjunto formado por los objetos útiles. - Una molécula de agua. 3. Denotar por extensión los siguientes conjuntos: - El conjunto formado por los nombres de los dedos de la mano. - El conjunto formado por los números naturales menores que 9. - El co...