Números enteros

Qué tal matemáticos, en esta ocasión les explico los números enteros, sus propiedades y los tipos de operaciones con números enteros.

La propiedad asociativa hace que si en la multiplicación
                                                      2 x 4 x 3 = 24
se reemplazan los factores 2 y 4 por su producto 8, el resultado de la operación varía: 

 8 x 3 = 24

La división es uniforme. El resultado de la división de dos números el único. Dividiendo miembro a miembro dos igualdades, se obtiene otra igualdad, por eso se llama uniforme:

Si         8 = 4 x 2

y          4 = 2 x 2

                        8 / 4 = (4 x 2) / ( 2 x 2)

       2 = 2

En el conjunto de los números naturales existe una condición para poder realizar la resta: el minuendo debe ser mayor o igual que el sustraendo. Cuando el sustraendo es mayor que el minuendo, su realización se hace imposible.
La solución a este problema consiste en considerar la existencia de números negativos (menores que cero). Por lo tanto, se puede definir como números enteros a cualquiera de los números positivos: +1, +2, +3, etc., o de los negativos: -1, -2, -3.
El conjunto de los números enteros se indica con Z.

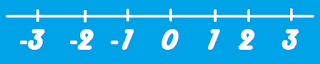
Z = {... , -3 , -2 , -1 , 0 , +1 , +2 , +3 , ... }

Cada elemento del conjunto Z es un número entero.
Los números enteros precedidos por el signo + se llaman positivos, y los que llevan delante el signo -, negativos. Los números naturales del conjunto N, contenidos todos ellos en el conjunto Z, se consideran enteros positivos.
Todo número entero expresa un valor relativo y un valor absoluto. El valor relativo está determinado por el signo. El valor absoluto de un número entero es el número natural que lo representa, independientemente del signo. Se indica con el signo | |.

Por ejemplo:
|+6| = 6 y |-7| = 7, que se lee de la siguiente manera: el valor absoluto del número entero positivo 6 es 6, y el valor absoluto del número entero negativo -7 es 7.

Dos números enteros son opuestos cuando tienen el mismo valor absoluto y distinto signo. Así:  17 y -17 son números opuestos; también -8 y 8.

Las propiedades
Los números enteros pueden cumplir propiedades de igualdad o de desigualdad, que son las siguientes: 

Dos números enteros son iguales cuando tienen el mismo signo e igual valor absoluto. Por ejemplo: -3 = 3 si el valor absoluto de |-3| = |-3| y el signo de -3 es igual al de -3.

Un número entero positivo es mayor (>) que otro también positivo cuando el primero tiene mayor valor absoluto que el segundo.
De esta manera , +30 > +28; +7 > +5.

Un número entero negativo es mayor que otro también negativo cuando el primero tiene menor valor absoluto que el segundo.
Así: -8 > -11 , pues |-8| = 8 |-11| = 11.

Un número entero positivo siempre es mayor que cualquier otro negativo. Por ejemplo: +7 > -9.

Un número entero positivo es menor (<) que otro también positivo cuando el primero tiene valor absoluto que el segundo. Puede verse claramente en este ejemplo:

  +2 < +15

Un número entero negativo es menor que otro también negativo, cuando el primero tiene mayor valor absoluto que el segundo, a saber: -10 < -8.
Un número entero negativo es siempre menor que cualquier entero positivo. Por ejemplo: -6 < +2.

Operaciones con números enteros

La suma o adición de números enteros se efectúa de acuerdo con las siguientes reglas: 
La suma de dos enteros positivos es otro entero positivo, cuyo valor absoluto es la suma de los valores absolutos de los sumandos.
Por ejemplo: 

(+8) + (+4) = +12

(+3) + (+5) + (+10) = +18

La suma de dos enteros negativos es igual a otro entero negativo, cuyo valor absoluto es la suma de los valores absolutos de los sumandos:

(-9) + (-2) = -11

(-3) + (-4) + (-5) = -12

La suma de do números enteros, uno positivo y otro negativo, es igual a otro entero, cuyo signo es el del sumando de mayor valor absoluto y cuyo valor absoluto es la diferencia de los valores absolutos de los números dados.
Por ejemplo:

(+20) + (-7) = +13

(-80) + (+10) = -70

Aplicando esta última definición es que la suma de números enteros opuestos es igual a 0:

(+5) + (-5) = 0

La suma de los números enteros cumple las mismas propiedades que la suma de números naturales: es uniforme, conmutativa y asociativa.
La resta o sustracción de números enteros es siempre posible, pues no existen restricciones; lo que no ocurre en la sustracción de números naturales. La diferencia de dos números enteros es igual a otro número entero, de tal manera que sumando al segundo dé un resultado igual al primero:

(+5) - (-2) = +7  pues      (-2) + (+7) = +5

(-8) - (-3) = -5    pues       (-3) + (-5) = -8

Para restar dos números enteros se suma al minuendo el opuesto del sustraendo: 

(+8) - (+12) = (+8) + (-12) = -4

(-3) - (-7) = (-3) + (+7) = +4

La resta de números enteros la propiedad de uniformidad.
En la multiplicación o producto de números enteros se presentan tres casos: multiplicación de dos enteros positivos, multiplicación de dos enteros de distinto signo y multiplicación de dos enteros negativos.
El producto de dos enteros positivos es otro entero positivo, cuyo valor absoluto es el producto de los valores absolutos de los factores:

(+5) x (+6) = +30

(+3) x ( +9) = +27

El producto de dos enteros de distinto signo es un número entero negativo, cuyo valor absoluto es el producto de los valores absolutos de los factores:

(+8) x (-6) = -48

(-5) x (+9) = -45

El producto de dos enteros negativos es un entero positivo cuyo valor absoluto se obtiene multiplicando los valores absolutos de los factores:

(-5) x (-7) = +35

(-7) x (-9) = +63

El producto o la división de dos números enteros llevará el signo que corresponda, según la siguiente regla:

            + x + = +

            + x  - =  -

            -  x + =  -

              -  x  - = +  

En cuanto a la división, el cociente exacto de dos números enteros es igual a un tercer número entero tal que, multiplicado por el divisor, dé un producto igual al dividendo.

Si te gustó, compártelo 
¿Crees que me faltó algo?, deja tu comentario :)