Ejercicios de Conjuntos - Parte 2

1. Verificar que los conjuntos A y B son iguales, siendo:

A = { x ∈ N / x es par y x < 9 } , B = { x ∈ N / x es par y x ≤ 70 }

2. Indicar si las siguientes afirmaciones son verdaderas o falsas:

- a ∈ { a }
- a ⊂ { a }
- Ø ⊂ { a }
- Ø ∈ { a, Ø }
- Ø ⊂ { a, Ø }
- { a } ⊂ Ø

3. Sea: A = { 1, 2, 3 }

- Denotar por extensión el conjunto de las partes de A.
- Decir si son verdaderas o falsas las siguientes proposiciones:

Ø ∈ P (A), { 1 } ∈ P (A), A ∈ P (A), Ø ⊂ P (A), { 1 } ⊂ P (A), P (A) ∈ P (A).

4. Sean los siguientes conjuntos:

A = { 1 , 2 }, B = { 1 , 3 } y C = { A, B, 1 , 2 }

Indicar si son verdaderas o falsas las siguientes proposiciones:

1. 1 ∈ A 
2. A ⊂ C
3. Ø ∈ C
4. 1 ∈ C
5. B ∈ C
6. Ø ⊂ c
7. A ∈ A
8. 3 ∈ B
9. A = B
10. A ⊂ A
11. 3 ∈ C
12. 3 ⊂ B

5. Investigar si son iguales los siguientes pares de conjuntos:

A = {  x ∈ N / 1 ≤ x < 5 }
B = { x ∈ N / x es divisor de 24 } 
C = {  x ∈ N / x²  es par }
D = {  x ∈ N / x es par }

6. Obtener el conjunto de partes de cada uno de los siguientes conjuntos:

A = { 0 }
B = {{ a }}, a }
C= Ø 

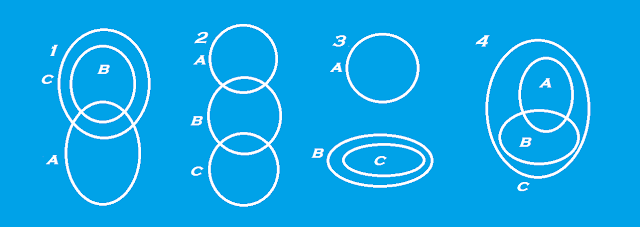
7. Definir por extensión conjuntos cuya representación en diagramas de Venn 
sea:

8. Representar los siguientes conjuntos mediante diagramas de Venn:

U = { x ∈ N / 10 < x ≤ 20 }
B = { x ∈ U / x es múltiplo de 3 }
A = { x ∈ N / 10 < x ≤ 15 }
C = { 11 , 13 , 15 , 19 , 20 }

9. Teniendo en cuenta el gráfico, decir si son verdaderas o falsas las siguientes proposiciones:

a ∈ α , S ∈ ß , T ∈ α , A ∈ α , r ∈ ß , r ∈ α ,                   
P ∈ α , Q ∈ ß , Q ∈ α , P ∈ r , A ∈ α , P ∈ ß

10. Sea: A = { x/x fue presidente de USA }. Analizar si las siguientes afirmaciones son verdaderas o falsas:

Obama ∈ A
{ Obama } ∈ A
{ Obama } ⊂ A
Maduro ∈ A
{ un pié de Obama } ⊂ A
{ Obama } ⊂ P(A)

11. Definir por extensión conjuntos cuya representación gráfica sea la siguiente:

12. Indicar de acuerdo con el dibujo si las siguientes afirmaciones son verdaderas o falsas:

13. De acuerdo con el dibujo del ejercicio anterior indicar si las siguientes afirmaciones son verdaderas o falsas:

14. Sean α (alfa) y ß (beta) dos planos. Analizar qué relación vincula a α y ß, si:

1. α ∩ ß = Ø
2. α ∩ ß = α 
3. α ∩ ß = r, donde r es una recta

15. Sean A = { 1 , 2 , 3 }, B = { 1 , 2 } y C = { 2 , 3 , 4 }. Completar la siguiente tabla:

16. Teniendo en cuenta el gráfico, indicar si las siguientes afirmaciones son verdaderas o falsas:

1. S [P , T] ⊂ A
2. α ∈ [α , b]
3. S [T , P] ⊂ α
4. r ⊂ S [α , X]
5. T ∈ S [ß , X]
6. P ∈ S [α , Q]
7. Q ∈ S [α , X]
8. r ⊂ S [r , B]

17. Considerando el siguiente gráfico, indicar si las siguientes afirmaciones son verdaderas o falsas.

α ⊂ π, AB ⊂ P(π)
A ∈ P(π), α ∈ P(π), A ∈ π, {A} ∈ P(π),
S [α , B} ⊂ π, S [α , B} ∈ P(π), {α} ∈ P(π)

18. Analizar si las siguientes afirmaciones son verdaderas o falsas:

1. {1} ∈ { 1 , 2 }
2. Ø ∈ {Ø}
3. Ø ⊂ {Ø}
4. A ⊂ A
5. A = A
6. {1} ∩ {{1} , 2} = {1}
7. {1} ∩ {1 , 2, 3} = {1}
8. Ø ⊂ A
9. {1} ⊂ {1 , 2}

19. Teniendo en cuenta el siguiente gráfico, clasificar en verdaderas o falsas las proposiciones:

1. a ∈ α
2. P ∈ α 
3. P ∈ a ∩ b
4. P = a ∩ b
5. C ∉ a}
6. a ⊂ a
7. a ⊂ A
8. {C} ∩ a = Ø
9. {P} = a ∩ b

20. Dado A = { x / x ∈ N y x + 1 ≤ 2 }
1. Denotar A por extensión 
2. Formar P(A)
3. Hallar P(A) ∩ {{0}} , A , 3 }

Encuentra más sobre Conjuntos AQUÍ.

*Estaré publicando más ejercicios*

Si te gustó, no olvides compartirlo! 
¿Crees que me faltó algo?, deja tu comentario :)