Números naturales - Parte 5
1. Determinar por divisiones sucesivas el mcd de los siguientes números:
3 481 y 203
500 y 60
1 200 y 400
2. Determinar el mcd por divisiones sucesivas entre:
44 y 198
143 y 650
7 553 y 8 383
253, 713 y 6 900
3. Determinar el mcd y el mcm, por descomposición en factores primos, entre:
340 y 250
850 y 280
14 y 58
10 y 30
4. Utilizando el método de las divisiones sucesivas determinar el mcd y el mcm de:
18 634 y 2 178
n + 1 y n
5. Determinar el mcm por descomposición en factores primos entre:
44 y 198
630 y 504
30 y 54
504, 350 y 9 000
6. Usando el mcd hallado en el ejercicio 3, hallar el mcm entre:
143 y 650
7 553 y 8 383
7. Calcular x sabiendo que:
mcd (8,x) = 8
mcd (6,x) = 2
mcm (3,x) = 6
mcm (x,x+1) = 12
8. Hallar x sabiendo que mcd (30,x) = 10 y mcm (30,x) = 240
9. Hallar x, e y sabiendo que:
x + y = 7 < y, mcd (x.y) = 1 y mcm (x,y) = 12
10. ¿Cuántos años bisiestos múltiplos de 5 hay en 4 siglos?¿Y múltiplos de 6?
11. Probar que los conjuntos A = N y B = { x ∈ N / x = 1 ∨ (x = 2ⁿ ∧ N > 1 ∧ n ∈ N) } tienen la misma cantidad de elementos.
12. Sean A = { x ∈ N / x < 2 } y B = { x ∈ N / 5 < x < 7 }. Hallar P ({(x,y) / x ∈ A ∧ y ∈ B}).
13. En A = { 0 , 1 , 2 , 3 } se hace corresponder a cada par de elementos de A el resto de la división entre la suma de ellos y 4.
a) Representar dicha operación mediante una tabla.
b) Decir si es conmutativa y si tiene elemento neutro.
14. Sea n ∈ N. Se define el símbolo "n!" que se lee n factorial o factorial de n, mediante
16. Probar que si sumamos una unidad al producto de dos números impares consecutivos, obtenemos un cuadrado perfecto.
17. Indicar qué paso es incorrecto en la siguiente demostración. Justificar la respuesta.
Sean a, b y c números naturales tales que:
18. ¿Cuál es la edad de una persona que dentro de tres años tendrá una edad tal que su cuadrado será la suma entre el séxtuplo de la que tiene actualmente y 10?
19. Resolver las siguientes ecuaciones en N:
20. Sean los conjuntos A = { x ∈ N / 3 | x ∧ 0 < x ≤ 82 } y B = { x ∈ A / 2 | x }. Si C es un subconjunto de A tal que B ∩ C tiene tres elementos y B ∪ C tiene 15 elementos, se pide:
a) Determinar el número de elementos de C.
b) Determinar el número de elementos de A - (B ∪ C).
*Estaré publicando más ejercicios*
Si te gustó, no olvides compartirlo!
¿Crees que me faltó algo?, deja tu comentario :)
3 481 y 203
500 y 60
1 200 y 400
2. Determinar el mcd por divisiones sucesivas entre:
44 y 198
143 y 650
7 553 y 8 383
253, 713 y 6 900
3. Determinar el mcd y el mcm, por descomposición en factores primos, entre:
340 y 250
850 y 280
14 y 58
10 y 30
4. Utilizando el método de las divisiones sucesivas determinar el mcd y el mcm de:
18 634 y 2 178
n + 1 y n
5. Determinar el mcm por descomposición en factores primos entre:
44 y 198
630 y 504
30 y 54
504, 350 y 9 000
6. Usando el mcd hallado en el ejercicio 3, hallar el mcm entre:
143 y 650
7 553 y 8 383
7. Calcular x sabiendo que:
mcd (8,x) = 8
mcd (6,x) = 2
mcm (3,x) = 6
mcm (x,x+1) = 12
8. Hallar x sabiendo que mcd (30,x) = 10 y mcm (30,x) = 240
9. Hallar x, e y sabiendo que:
x + y = 7 < y, mcd (x.y) = 1 y mcm (x,y) = 12
10. ¿Cuántos años bisiestos múltiplos de 5 hay en 4 siglos?¿Y múltiplos de 6?
11. Probar que los conjuntos A = N y B = { x ∈ N / x = 1 ∨ (x = 2ⁿ ∧ N > 1 ∧ n ∈ N) } tienen la misma cantidad de elementos.
12. Sean A = { x ∈ N / x < 2 } y B = { x ∈ N / 5 < x < 7 }. Hallar P ({(x,y) / x ∈ A ∧ y ∈ B}).
13. En A = { 0 , 1 , 2 , 3 } se hace corresponder a cada par de elementos de A el resto de la división entre la suma de ellos y 4.
a) Representar dicha operación mediante una tabla.
b) Decir si es conmutativa y si tiene elemento neutro.
14. Sea n ∈ N. Se define el símbolo "n!" que se lee n factorial o factorial de n, mediante
15. Simplificar las siguientes expresiones:
1. n! : (n - 3)!
2. (n! (n - 1)! ) : (n - 2)!²
3. (n! (n + 1)! ) : (n - 1)!16. Probar que si sumamos una unidad al producto de dos números impares consecutivos, obtenemos un cuadrado perfecto.
17. Indicar qué paso es incorrecto en la siguiente demostración. Justificar la respuesta.
Sean a, b y c números naturales tales que:
18. ¿Cuál es la edad de una persona que dentro de tres años tendrá una edad tal que su cuadrado será la suma entre el séxtuplo de la que tiene actualmente y 10?
19. Resolver las siguientes ecuaciones en N:
20. Sean los conjuntos A = { x ∈ N / 3 | x ∧ 0 < x ≤ 82 } y B = { x ∈ A / 2 | x }. Si C es un subconjunto de A tal que B ∩ C tiene tres elementos y B ∪ C tiene 15 elementos, se pide:
a) Determinar el número de elementos de C.
b) Determinar el número de elementos de A - (B ∪ C).
*Estaré publicando más ejercicios*
Si te gustó, no olvides compartirlo!
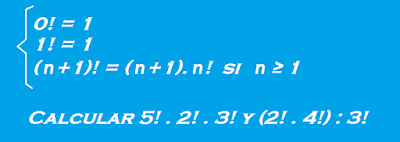






Comentarios
Publicar un comentario