Representación de un número decimal
Todos los días nos desplazamos de un lugar a otro, uno de ellos puede ser de la casa al colegio. Tú o alguno de tus amigos podrá decir, por ejemplo:
De mi casa al colegio hay 10 cuadras.
Para ir a pie de mi casa al colegio necesito 15 minutos.
Para ir en bicicleta de mi casa al colegio empleo 3 minutos.
En este caso se está haciendo un correspondencia numérica al recorrido de la casa al colegio.
A este tipo de correspondencia se denomina medir una distancia y al proceso, medición.
La medida o resultado de una medición se expresa mediante un número acompañado de una unidad de medida.
Así, en 10 cuadras, el número es 10 y la unidad de medida, la cuadra; en 15 minutos, el número es 15 y la unidad de medida, el minuto.
Entre otros ejemplos tenemos:
Hemos requerido 8 horas para llegar de Lima a Trujillo.
Un automóvil puede recorrer hasta 120 kilómetros por hora.
Jorge pesa 48 kilogramos.
En algunos lugares aún se usan algunas unidades primitivas de medida, tales como la libra, la onza, el pie, la pulgada, la yarda, etc.
Antes, por su sencillez, se usaban las unidades del Sistema Métrico Decimal (SMD). Luego se optó por el uso del Sistema Internacional de Unidades (SIU), cuyo uso obligatorio en Perú fue aprobado el 20 de Agosto de 1984.
Hasta aquí sólo hemos usado números naturales o enteros para medir cantidades. Pero en la vida real, cuando hay necesidad de medir, surge el problema de establecer una correspondencia precisa entre un objeto y un conjunto de medidas. Así, por ejemplo, para medir una pieza de tela tomamos como unidad de medida el metro. Sin embargo, es muy frecuente que una pieza de tela no tenga un número exacto de metros, sino por ejemplo, puede medir más de 2 metros pero no menor de 3 metros. Si esto ocurre, el metro ya no sirve como unidad de medida. Tendremos que tomar otra unidad de medida más pequeña tal como el decímetro, centímetro, etc.
NUMERO DECIMAL
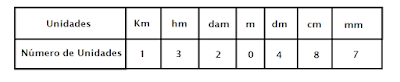
Esta tabla se ha llenado luego de haber medido un rollo de cordel.
Si se toma como unidad de medida el cm, escribimos: 132 048,7
Si se toma como unidad de medida el m, escribimos: 1 320,487
Si se toma como unidad de medida el km, escribimos: 1, 320 487
Como vemos, la ubicación de la coma dentro del número depende de la unidad de medida que se elija. Esta se toma generalmente de acuerdo a las necesidades. Así, si se desea medir la longitud de un lápiz, será cómodo usar el centímetro como unidad de medida; en cambio, si se trata de medir la longitud de una carretera, será conveniente usar el kilómetro.
A este tipo de escritura de un número, en base diez, llamamos escritura decimal del número o simplemente decimos que se trata de un número decimal.
En un número decimal tal como 25, 14 ; a 25 llamamos parte entera y a 14, parte decimal. Se lee: veinticinco enteros catorce centésimos o bien veinticinco enteros, un decimo, cuatro centésimos.
En general, un número decimal tiene la forma:
En 25,14 se tiene, a1=1 , a2=4
Además, un número decimal puede escribirse como una suma, en la siguiente forma:
25,14 = 20 + 5 + 0,1 + 0,04
-8,537 = -(8 + 0,5 + 0,03 + 0,007)
Este último se lee: N enteros, a1 décimos, a2 centésimos, ...
REPRESENTACION DE UN NUMERO DECIMAL EN LA RECTA NUMERICA
Observemos en las siguientes figuras, la representación de 0,8 y 2,4:
De estas figuras vemos que:
Si el número tiene una cifra decimal, el segmento que representa la unidad se divide en diez partes iguales, y de ellos se toma las que indica la cifra decimal.
Si el número tiene dos cifras decimales, el segmento unitario se divide en cien partes iguales y de ellas se toma las que indican esas dos cifras, etc.
COMPARACION DE NUMEROS DECIMALES
Recordemos que:
Todo número negativo es menor que todo número positivo ( -6<1,-1<2 ).
De dos números positivos, es menor el que tiene menor valor absoluto ( 3<4,8<12 ).
De dos números negativos, es menor el que tiene mayor valor absoluto ( -8<-5,-9<-8,-15<-1 ).
Para comparar dos números decimales se procede como sigue:
Se comparan partes enteras.
Si las partes enteras son iguales, se comparan las cifras de los décimos.
Si las cifras de los décimos son iguales, se comparan las cifras de los centésimos, y así sucesivamente.
8,45 < 9,21 porque 8 < 9
5,321 < 5,421 porque 0,3 < 0,4
15,486 < 15,465 porque 0,48 < 0,46 u 0,08 < 0,06
-10,54 < 0,54 porque -10 < 0
-16,045 < -35,18 porque -16 < -35
FRACCIONES DECIMALES
Son fracciones de la forma:
Así, son fracciones decimales:
Toda fracción decimal admite una representación decimal inmediata; tales como:
2/10 = 0,2
35/100 = 30/100 + 5/100 = 3/10 + 5/100 = 0,3 + 0,05 = 0,35
De aquí la lectura: treinta y cinco centésimos o bien tres décimos, cinco centésimos.
358/100=300/100+50/100+8/100 = 3+5/10+8/100 = 3+0,5+0,08=3,58
-236/1000=-200/1000+-30/1000+-6/1000= -2/10+-3/100+-6/1000 = -0,236
De estos ejemplos deducimos que para escribir en forma decimal una fracción dada, cuyo denominador es una potencia de 10, se escribe el numerador y a partir de la última cifra de la derecha se separan mediante la coma decimal tantas cifras como ceros tenga ducha potencia.
Así, en 358/100 se escribe 358 y se separan dos cifras contadas a partir del 8, quedando 3,58 (por haber 100 en el denominador).
En 35/100000 se escribe 35 y contando a partir del 5 se cuenta cinco cifras, pero como sólo hay dos de ellos (5 y 3) se completa con ceros, resultando 0,00035.
La fracción que da origen a un número decimal se llama generatriz o primitiva de dicho número decimal. Así, 2/10 es la generatriz de 0,2.
No toda fracción es decimal, sin embargo, toda fracción admite una representación decimal, que se obtiene al dividir el numerador entre el denominador.
La representación decimal o número decimal de una fracción puede ser exacta, periódica pura o periódica mixta.
Un número decimal es exacto si posee un determinado número de dígitos, el último de los cuales es necesariamente diferente de cero, tales como:
Un número decimal es periódico puro si está formado por bloques de dígitos (períodos), que se repiten indefinidamente a partir del punto decimal, tales como:
Un número decimal es periódico mixto si a partir de un cierto número de dígitos a la derecha del punto decimal, se presentan bloques o periodos que se repiten indefinidamente, tales como:
FORMAS DE RECONOCER EL NUMERO DECIMAL QUE DARA ORIGEN A UNA FRACCION IRREDUCTIBLE
Si el denominador de una fracción es de la forma:
con r y s números naturales, el número decimal correspondiente es exacto.
Si el denominador de una fracción se descompone en factores primos diferentes de 2 y 5, el número decimal correspondiente es periódico puro.
Si el denominador de una fracción admite como factores primos además de 2 ó 5, otros factores, el número decimal correspondiente es periódico mixto.
Entendiste este tema?
¿A qué llamamos número decimal?
¿Cómo se representa un número decimal en la recta numérica?
¿Cómo se procede para comparar dos números decimales?
¿Qué es una fracción decimal?
¿Qué diferencia hay entre un número decimal periódico puro y un número decimal periódico mixto?
Dada una fracción irreductible ¿Cómo se reconoce el número decimal al que da origen?
Ejercicios:
De mi casa al colegio hay 10 cuadras.
Para ir a pie de mi casa al colegio necesito 15 minutos.
Para ir en bicicleta de mi casa al colegio empleo 3 minutos.
En este caso se está haciendo un correspondencia numérica al recorrido de la casa al colegio.
A este tipo de correspondencia se denomina medir una distancia y al proceso, medición.
La medida o resultado de una medición se expresa mediante un número acompañado de una unidad de medida.
Así, en 10 cuadras, el número es 10 y la unidad de medida, la cuadra; en 15 minutos, el número es 15 y la unidad de medida, el minuto.
Entre otros ejemplos tenemos:
Hemos requerido 8 horas para llegar de Lima a Trujillo.
Un automóvil puede recorrer hasta 120 kilómetros por hora.
Jorge pesa 48 kilogramos.
En algunos lugares aún se usan algunas unidades primitivas de medida, tales como la libra, la onza, el pie, la pulgada, la yarda, etc.
Antes, por su sencillez, se usaban las unidades del Sistema Métrico Decimal (SMD). Luego se optó por el uso del Sistema Internacional de Unidades (SIU), cuyo uso obligatorio en Perú fue aprobado el 20 de Agosto de 1984.
Hasta aquí sólo hemos usado números naturales o enteros para medir cantidades. Pero en la vida real, cuando hay necesidad de medir, surge el problema de establecer una correspondencia precisa entre un objeto y un conjunto de medidas. Así, por ejemplo, para medir una pieza de tela tomamos como unidad de medida el metro. Sin embargo, es muy frecuente que una pieza de tela no tenga un número exacto de metros, sino por ejemplo, puede medir más de 2 metros pero no menor de 3 metros. Si esto ocurre, el metro ya no sirve como unidad de medida. Tendremos que tomar otra unidad de medida más pequeña tal como el decímetro, centímetro, etc.
NUMERO DECIMAL
Esta tabla se ha llenado luego de haber medido un rollo de cordel.
Si se toma como unidad de medida el cm, escribimos: 132 048,7
Si se toma como unidad de medida el m, escribimos: 1 320,487
Si se toma como unidad de medida el km, escribimos: 1, 320 487
Como vemos, la ubicación de la coma dentro del número depende de la unidad de medida que se elija. Esta se toma generalmente de acuerdo a las necesidades. Así, si se desea medir la longitud de un lápiz, será cómodo usar el centímetro como unidad de medida; en cambio, si se trata de medir la longitud de una carretera, será conveniente usar el kilómetro.
A este tipo de escritura de un número, en base diez, llamamos escritura decimal del número o simplemente decimos que se trata de un número decimal.
En un número decimal tal como 25, 14 ; a 25 llamamos parte entera y a 14, parte decimal. Se lee: veinticinco enteros catorce centésimos o bien veinticinco enteros, un decimo, cuatro centésimos.
En general, un número decimal tiene la forma:
En 25,14 se tiene, a1=1 , a2=4
Además, un número decimal puede escribirse como una suma, en la siguiente forma:
25,14 = 20 + 5 + 0,1 + 0,04
-8,537 = -(8 + 0,5 + 0,03 + 0,007)
Este último se lee: N enteros, a1 décimos, a2 centésimos, ...
REPRESENTACION DE UN NUMERO DECIMAL EN LA RECTA NUMERICA
Observemos en las siguientes figuras, la representación de 0,8 y 2,4:
De estas figuras vemos que:
Si el número tiene una cifra decimal, el segmento que representa la unidad se divide en diez partes iguales, y de ellos se toma las que indica la cifra decimal.
Si el número tiene dos cifras decimales, el segmento unitario se divide en cien partes iguales y de ellas se toma las que indican esas dos cifras, etc.
COMPARACION DE NUMEROS DECIMALES
Recordemos que:
Todo número negativo es menor que todo número positivo ( -6<1,-1<2 ).
De dos números positivos, es menor el que tiene menor valor absoluto ( 3<4,8<12 ).
De dos números negativos, es menor el que tiene mayor valor absoluto ( -8<-5,-9<-8,-15<-1 ).
Para comparar dos números decimales se procede como sigue:
Se comparan partes enteras.
Si las partes enteras son iguales, se comparan las cifras de los décimos.
Si las cifras de los décimos son iguales, se comparan las cifras de los centésimos, y así sucesivamente.
8,45 < 9,21 porque 8 < 9
5,321 < 5,421 porque 0,3 < 0,4
15,486 < 15,465 porque 0,48 < 0,46 u 0,08 < 0,06
-10,54 < 0,54 porque -10 < 0
-16,045 < -35,18 porque -16 < -35
FRACCIONES DECIMALES
Son fracciones de la forma:
Así, son fracciones decimales:
Toda fracción decimal admite una representación decimal inmediata; tales como:
2/10 = 0,2
35/100 = 30/100 + 5/100 = 3/10 + 5/100 = 0,3 + 0,05 = 0,35
De aquí la lectura: treinta y cinco centésimos o bien tres décimos, cinco centésimos.
358/100=300/100+50/100+8/100 = 3+5/10+8/100 = 3+0,5+0,08=3,58
-236/1000=-200/1000+-30/1000+-6/1000= -2/10+-3/100+-6/1000 = -0,236
De estos ejemplos deducimos que para escribir en forma decimal una fracción dada, cuyo denominador es una potencia de 10, se escribe el numerador y a partir de la última cifra de la derecha se separan mediante la coma decimal tantas cifras como ceros tenga ducha potencia.
Así, en 358/100 se escribe 358 y se separan dos cifras contadas a partir del 8, quedando 3,58 (por haber 100 en el denominador).
En 35/100000 se escribe 35 y contando a partir del 5 se cuenta cinco cifras, pero como sólo hay dos de ellos (5 y 3) se completa con ceros, resultando 0,00035.
La fracción que da origen a un número decimal se llama generatriz o primitiva de dicho número decimal. Así, 2/10 es la generatriz de 0,2.
No toda fracción es decimal, sin embargo, toda fracción admite una representación decimal, que se obtiene al dividir el numerador entre el denominador.
La representación decimal o número decimal de una fracción puede ser exacta, periódica pura o periódica mixta.
Un número decimal es exacto si posee un determinado número de dígitos, el último de los cuales es necesariamente diferente de cero, tales como:
2,45 ; 0,48 ; 125,004 ; -2,305 ; -6,125
Un número decimal es periódico puro si está formado por bloques de dígitos (períodos), que se repiten indefinidamente a partir del punto decimal, tales como:
Un número decimal es periódico mixto si a partir de un cierto número de dígitos a la derecha del punto decimal, se presentan bloques o periodos que se repiten indefinidamente, tales como:
FORMAS DE RECONOCER EL NUMERO DECIMAL QUE DARA ORIGEN A UNA FRACCION IRREDUCTIBLE
Si el denominador de una fracción es de la forma:
con r y s números naturales, el número decimal correspondiente es exacto.
Si el denominador de una fracción se descompone en factores primos diferentes de 2 y 5, el número decimal correspondiente es periódico puro.
Si el denominador de una fracción admite como factores primos además de 2 ó 5, otros factores, el número decimal correspondiente es periódico mixto.
Entendiste este tema?
¿A qué llamamos número decimal?
¿Cómo se representa un número decimal en la recta numérica?
¿Cómo se procede para comparar dos números decimales?
¿Qué es una fracción decimal?
¿Qué diferencia hay entre un número decimal periódico puro y un número decimal periódico mixto?
Dada una fracción irreductible ¿Cómo se reconoce el número decimal al que da origen?
Ejercicios:
1. Dar cinco ejemplos que muestren la utilidad de los números naturales o de los enteros para medir magnitudes.
2. Dar cinco ejemplos que muestren que los números naturales o los enteros no son suficientes para medir magnitudes y que es necesario usar los números decimales.
3. Leer los siguientes números decimales:
2,25 ; -1,4 ; 5,125 ; -6,04 ; 8,001 ; -5,008 ; 0,00245 ; 0,01004
4. Escribir los siguientes números decimales:
a) Tres enteros catorce centésimos.
b) Veinte enteros quince milésimos.
c) Menos diez enteros ciento cuatro milésimos.
d) Ochocientos doce diez milésimos.
e) Cuatrocientos veintidós cien milésimos.
5. Escribir y leer cinco números positivos y cinco negativos.
6. Representar los siguientes números decimales:
1,2 ; -1,5 ; 2,25 ; -0,45 ; 3,5
7. Indicar las unidades de medida que es conveniente usar para medir.
a) Largo y ancho de una puerta.
b) Estatura de una persona.
c) Largo, ancho y altura de una caja de zapatos.
d) Peso de una persona.
e) Peso de los medicamentos, tales como pastillas, cápsulas, etc.
f) Tiempo que toma un automóvil en llegar de Tacna a Lima.
g) Profundidad a la que está un submarino a una hora y día señalado.
h) Altura a la que puede elevarse un avión.
8. Completar la siguiente tabla con: < , = ó >, según corresponda.
9. Escribir diez ejemplos de fracciones decimales.
10. Dar diez fracciones decimales y escribirlos en forma de número decimal.
11. Dar diez fracciones y escribirlas en forma de número decimal.
12. Completar la siguiente tabla:
13. Escribir diez fracciones que den origen a un número decimal exacto.
14. Dar diez fracciones que originen un número decimal periódico puro.
15. Dar diez fracciones que originen un número decimal periódico mixto.
16. Ordenar de menor a mayor los números:
a) -3,42 ; 0,84 ; -1,01 ; 9,05 ; 9,008
b) 4,6 ; -5,08 ; -4,06 ; -5,09 ; 4,61
c) 0,5 ; 2/3 ; 8/9 ; -1,5 ; 3/4 ; 1 2/9
d) -4/3 ; -1/3 ; 5/8 ; 0,048 ; 2,01 ; 4/3 ; 2,1
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)
¿Crees que me faltó algo?, deja tu comentario :)
















Comentarios
Publicar un comentario