Multiplicación de fracciones
MULTIPLICACION DE UN NUMERO NATURAL POR UNA FRACCION
OPERACIONES COMBINADAS DE ADICION, SUSTRACCION Y MULTIPLICACION
Al igual que para las operaciones combinadas de números naturales y enteros, primero se realiza las multiplicaciones y luego las operaciones de adición y sustracción. Cuando hay signos de colección, primero se realiza las operaciones indicadas dentro de estos, comenzando por los interiores.
Ejemplo:
Entendiste este tema?
¿Cómo se multiplíca un número natural por una fracción?
¿Cómo se multiplíca un fracción por un número natural?
¿Cómo se halla el producto de dos o más fracciones?
¿Cómo se multiplíca dos o más números mixtos?
¿Cómo se halla el producto de tres o más fracciones?
Si buscas División de Fracciones entra aquí.
Ejercicios:
1. Completar la siguiente tabla:
2. Completar la siguiente tabla:
3. Efectuar:
a) 4/9 x 18/7 x 21/8
b) 5/13 x 26/25 x 13/4 x 15/39
c) 14/17 x 51/28 x 4/9 x 3/5
d) 5 1/4 x 2 2/3 x 4 1/2 x 3 3/4
4. Efectuar:
a) ( 1 - 3/8 ) x 3 1/5
b) ( 5 1/4 x 1/8 - 1/5 ) x 3 7/11
c) ( 9 3/4 x 5 1/4 - 4 ) x ( 2 - 3/2 )
d) ( 5 2/7 - 3 1/3 + 5/21 ) x ( 4 1/2 - 2 1/4 )
e) ( 3/5 x 5/6 + 3 1/2 ) x ( 2 1/4 x 5 1/3 )
f) ( 2 1/3 x 4 2/3 - 5 2/5 ) x ( 3 1/4 - 2 1/5 )
g) ( 4 1/5 x 3 1/8 - 5 5/8 ) x ( 2 1/3 x 4 2/3 - 8/9 )
h) ( 2 - 1/3 + 3 1/5 x 2 1/2 ) x ( 5/8 x 1 1/7 - 2 3/7 )
i) ( 4 1/4 x 2 1/17 - 3 1/4 x 3 ) x ( 2 1/4 x 5 2/9 - 4 5/8 )
j) ( 2 1/4 - 1 2/5 x 4 4/5 + 3 2/5 ) x ( 9 1/8 - 2/9 x 8/3 x 27/16 )
5. Si el metro de una determinada tela cuesta 80 soles, ¿Cuánto se debe pagar por 3/4 de metro de esta tela?
6. Si el metro de tela para uniforme cuesta 30 soles, ¿Cuánto se debe pagar pr 4 metros y medio?
7. El metro de Dacrón (fibra sintética de poliéster) cuesta 48 soles y el de Popelina (tela delgada), 20 soles, ¿Cuánto se debe pagar por 2 metros y medio de Dacrón y un metro un cuarto de Popelina?
8. Jorge tiene dos metros un cuarto de tela para pantalón. Si hace confeccionar el suyo en el que entra la mitad de esta tela, ¿Cuánto le queda?
9. En un hogar, donde hay 8 niños se sabe que cada uno come pan y medio. ¿Cuántos panes comen diariamente estos niños?
10. Se desea hacer dos ventanas con marcos de aluminio. Una es de un metro y medio de ancho y un metro de altura, y la otra de un metro un cuarto de ancho y metro y medio de alto, ¿Cuál es la mínima longitud total de aluminio empleado?
11. Un comerciante compra un lote de mercadería por 24000 soles y vende dicha mercadería por los 5/4 del costo. ¿Cuánto recibe en total y cuál es su ganancia?
12. Con 100 soles que tenía, compré un pantalón por 16 soles y útiles escolares con la cuarta parte del resto. ¿Cuánto gasté en útiles escolares y cuánto me queda?
13. Un contratista toma una obra con el compromiso de terminarla a lo más en tres semanas. Si la primera semana hace la tercera parte y la segunda, 1/3 del resto, ¿Qué parte de la obra debe hacer la tercera semana?
14. La distancia de Lima a Trujillo es 546 Km. Un viajero, por diversas razones, llegó de Lima a Trujillo en tres días, caminando el primer día la tercera parte; el segundo día la mitad del resto; y el tercer día, el resto. ¿Qué distancia camina cada dia dicho viajero?
15. De una soga de 120 metros se han cortado dos trozos de cada una de las siguientes medidas 15 1/4 m, 18 2/5 m, 16 3/5 m y 5 1/4 m. ¿Cuánto sobra de soga?
16. Alberto es dueño de la 3/4 partes de las acciones de una empresa. Si vende los 4/5 de sus acciones, ¿Qué parte de acciones de la empresa no es ahora de Alberto?
17. Rosa tiene los 3/4 de la edad de Ana. Si esta tiene 30 años, ¿Qué edad tiene Rosa?
18. La distancia de Tacna a Tumbes es de 2640 km. Un viajero que va de Tacna a Tumbes, durante 5 días recorre como sigue: el primero, la quinta parte del total; el segundo, la cuarta parte del resto; el tercero, la tercera parte del resto; el cuarto, la mitad del resto; y el quinto, el resto. ¿Cuánto recorre diariamente?
19. Juan desea medir el largo y ancho de su sala y no dispone de un metro o regla graduada. Sin embargo, sabe que la distancia máxima entre las yemas de sus dedos, pulgar y meñique, es de un cuarto de metro (por lo que se le llama "cuarta" a esta distancia). Al medir encuentra que la sala tiene 18 cuartos de largo y 14 de ancho. ¿Cuál es el largo y ancho de dicha sala en metros?
20. Hugo tiene 35 años. ¿Cuántos años hace que Hugo tenía los 3/5 de su edad actual?
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)
Recordemos que:
El doble de 4 se escribe 2 x 4 que significa 2 veces. Esto es 2 x 4 = 4 + 4
El doble de 5 se escribe 3 x 5 que significa 3 veces. Esto es 3 x 5 = 5 + 5 + 5
Similarmente:
El doble de 1/3 se escribe 2 x 1/3 que significa 2 veces más 1/3. Esto es:
El triple de 2/9 se escribe 3 x 2/9 que significa 3 veces 2/9. Esto es:
Observemos que la palabra "de" se traduce por el signo x de multipliciación.
El cuádruple de 2/5 se escribe 4 x 2/5 que significa 4 veces 2/5. Esto es:
Para multiplicar un número natural por una fracción se multiplica el número natural por el numerador de la fracción y al producto se le coloca como denominador, el denominador de dicha fracción.
MULTIPLICACION DE UNA FRACCION POR UN NUMERO NATURAL
La mitad de 5 se escribe 1/2 x 5
Para hallar 1/2 x 5 tomamos en la recta numérica o en una cinta 5 unidades.
Cada unidad la dividimos en 2 partes de igual longitud. Tomamos la mitad de todas estas partes, es decir 5/2. Entonces:
1/2 x 5 = 5/2
Las 3/4 de 80 se obtiene:
¿Cómo se enuncia esta igualdad?
MULTIPLICACION DE DOS FRACCIONES
Hallar 1/3 de 1/2
Entonces, 1/3 de 1/2 se escribe 1/3 x 1/2
Gráficamente tenemos que:
La parte sombreada representa 1/2 de la unidad.
Esta parte sombreada la dividimos en 3 partes iguales.
La parte doblemente sombreada representa:
1/3 de 1/2 esta es 1/3 x 1/2
Por consiguiente 1/3 x 1/2 = 1/6
Hallar los 3/4 de 5/7
Entonces, 3/4 de 5/7 se escribe 3/4 x 5/7
Si a/b y c/d son dos fracciones cualesquiera, entonces:
Para multiplicar dos (o más) fracciones se multiplican numeradores u denominadores, respectivamente, formando la fracción producto con estos productos.
MULTIPLICACION DE NUMEROS MIXTOS
Se convierten los mixtos a fracciones y luego se efectúa la multiplicación:
¿Cómo se simplifican las fracciones en un producto indicado?
Si en un producto indicado de fracciones el numerador de una de ellas y el denominador de la misma o de la otra fracción tienen un divisor común, se dividen simultáneamente entre dicho divisor común y luego se multiplican numeradores y denominadores, respectivamente.
Ejemplo:
PROPIEDADES DE LA MULTIPLICACION DE FRACCIONES
1. Propiedad de Clausura
2. Propiedad Asociativa
3. El neutro multiplicativo es 1 o una fracción con numerador y denominador iguales:
4. Si a/b ≠ 0, entonces existe la fracción b/a llamada simétrico o inverso multiplicativo a a/b, así:
5. Propiedad conmutativa - El orden de los factores no altera el producto.
¿Cómo se efectúa el producto indicado de dos o más fracciones?
Se multiplican los numeradores y denominadores y luego se realiza la multiplicación de numeradores y denominadores, respectivamente.
Ejemplos:
OPERACIONES COMBINADAS DE ADICION, SUSTRACCION Y MULTIPLICACION
Al igual que para las operaciones combinadas de números naturales y enteros, primero se realiza las multiplicaciones y luego las operaciones de adición y sustracción. Cuando hay signos de colección, primero se realiza las operaciones indicadas dentro de estos, comenzando por los interiores.
Ejemplo:
Entendiste este tema?
¿Cómo se multiplíca un número natural por una fracción?
¿Cómo se multiplíca un fracción por un número natural?
¿Cómo se halla el producto de dos o más fracciones?
¿Cómo se multiplíca dos o más números mixtos?
¿Cómo se halla el producto de tres o más fracciones?
Si buscas División de Fracciones entra aquí.
Ejercicios:
1. Completar la siguiente tabla:
2. Completar la siguiente tabla:
3. Efectuar:
a) 4/9 x 18/7 x 21/8
b) 5/13 x 26/25 x 13/4 x 15/39
c) 14/17 x 51/28 x 4/9 x 3/5
d) 5 1/4 x 2 2/3 x 4 1/2 x 3 3/4
4. Efectuar:
a) ( 1 - 3/8 ) x 3 1/5
b) ( 5 1/4 x 1/8 - 1/5 ) x 3 7/11
c) ( 9 3/4 x 5 1/4 - 4 ) x ( 2 - 3/2 )
d) ( 5 2/7 - 3 1/3 + 5/21 ) x ( 4 1/2 - 2 1/4 )
e) ( 3/5 x 5/6 + 3 1/2 ) x ( 2 1/4 x 5 1/3 )
f) ( 2 1/3 x 4 2/3 - 5 2/5 ) x ( 3 1/4 - 2 1/5 )
g) ( 4 1/5 x 3 1/8 - 5 5/8 ) x ( 2 1/3 x 4 2/3 - 8/9 )
h) ( 2 - 1/3 + 3 1/5 x 2 1/2 ) x ( 5/8 x 1 1/7 - 2 3/7 )
i) ( 4 1/4 x 2 1/17 - 3 1/4 x 3 ) x ( 2 1/4 x 5 2/9 - 4 5/8 )
j) ( 2 1/4 - 1 2/5 x 4 4/5 + 3 2/5 ) x ( 9 1/8 - 2/9 x 8/3 x 27/16 )
5. Si el metro de una determinada tela cuesta 80 soles, ¿Cuánto se debe pagar por 3/4 de metro de esta tela?
6. Si el metro de tela para uniforme cuesta 30 soles, ¿Cuánto se debe pagar pr 4 metros y medio?
7. El metro de Dacrón (fibra sintética de poliéster) cuesta 48 soles y el de Popelina (tela delgada), 20 soles, ¿Cuánto se debe pagar por 2 metros y medio de Dacrón y un metro un cuarto de Popelina?
8. Jorge tiene dos metros un cuarto de tela para pantalón. Si hace confeccionar el suyo en el que entra la mitad de esta tela, ¿Cuánto le queda?
9. En un hogar, donde hay 8 niños se sabe que cada uno come pan y medio. ¿Cuántos panes comen diariamente estos niños?
10. Se desea hacer dos ventanas con marcos de aluminio. Una es de un metro y medio de ancho y un metro de altura, y la otra de un metro un cuarto de ancho y metro y medio de alto, ¿Cuál es la mínima longitud total de aluminio empleado?
11. Un comerciante compra un lote de mercadería por 24000 soles y vende dicha mercadería por los 5/4 del costo. ¿Cuánto recibe en total y cuál es su ganancia?
12. Con 100 soles que tenía, compré un pantalón por 16 soles y útiles escolares con la cuarta parte del resto. ¿Cuánto gasté en útiles escolares y cuánto me queda?
13. Un contratista toma una obra con el compromiso de terminarla a lo más en tres semanas. Si la primera semana hace la tercera parte y la segunda, 1/3 del resto, ¿Qué parte de la obra debe hacer la tercera semana?
14. La distancia de Lima a Trujillo es 546 Km. Un viajero, por diversas razones, llegó de Lima a Trujillo en tres días, caminando el primer día la tercera parte; el segundo día la mitad del resto; y el tercer día, el resto. ¿Qué distancia camina cada dia dicho viajero?
15. De una soga de 120 metros se han cortado dos trozos de cada una de las siguientes medidas 15 1/4 m, 18 2/5 m, 16 3/5 m y 5 1/4 m. ¿Cuánto sobra de soga?
16. Alberto es dueño de la 3/4 partes de las acciones de una empresa. Si vende los 4/5 de sus acciones, ¿Qué parte de acciones de la empresa no es ahora de Alberto?
17. Rosa tiene los 3/4 de la edad de Ana. Si esta tiene 30 años, ¿Qué edad tiene Rosa?
18. La distancia de Tacna a Tumbes es de 2640 km. Un viajero que va de Tacna a Tumbes, durante 5 días recorre como sigue: el primero, la quinta parte del total; el segundo, la cuarta parte del resto; el tercero, la tercera parte del resto; el cuarto, la mitad del resto; y el quinto, el resto. ¿Cuánto recorre diariamente?
19. Juan desea medir el largo y ancho de su sala y no dispone de un metro o regla graduada. Sin embargo, sabe que la distancia máxima entre las yemas de sus dedos, pulgar y meñique, es de un cuarto de metro (por lo que se le llama "cuarta" a esta distancia). Al medir encuentra que la sala tiene 18 cuartos de largo y 14 de ancho. ¿Cuál es el largo y ancho de dicha sala en metros?
20. Hugo tiene 35 años. ¿Cuántos años hace que Hugo tenía los 3/5 de su edad actual?
Más temas de Fracciones:
Si te gustó, compártelo
¿Crees que me faltó algo?, deja tu comentario :)

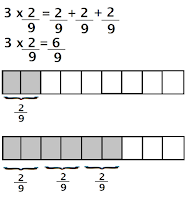



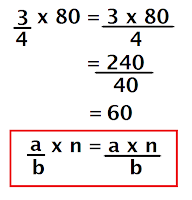
























Comentarios
Publicar un comentario